Leaf optical properties models
page updated on March 24th, 2006
While experimental measurements of leaf optical properties
were progressing, deterministic approaches based on diverse representations
of light interactions with plant leaves were also developed. These
models are distinguished by the underlying physics and by the
complexity of the leaf. The simplest ones consider the blade as
a single scattering and absorbing layer. In the most complicated
ones, all the cells are described in detail (shape, size, position,
and biochemical content). Whatever the approach, these models
have improved our understanding of the interactions of light with
plant leaves. They can be categorised into different classes,
arranged in order of increasing complexity:
Plate models
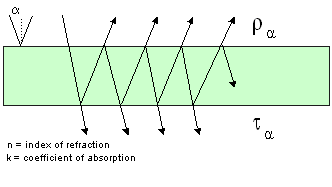
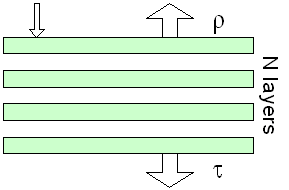 The
first plate model was introduced by Allen
et al. (1969) who represented a leaf as an absorbing plate
with rough surfaces giving rise to Lambertian diffusion. Parameters
here are an index of refraction and an absorption coefficient.
This model was successful in reproducing the reflectance spectrum
of a compact corn leaf characterised by few air-cell wall interfaces.
The same authors rapidly extended the model to non-compact leaves
by regarding them as piles of N plates separated by N-1 air spaces
(Allen et al., 1970). The solution
of such a system, provided in the last century by Stokes (1862),
has been extended to N being a real number: this is the so-called
generalised plate model. This additional parameter N actually
describes the leaf internal structure and plays a role similar
to that of the scattering coefficients in the Kubelka-Munk model.
Now in widespread use in the remote sensing community, the PROSPECT model (Leaf Optical Properties
Spectra) has been designed this way (Jacquemoud and Baret,
1990). It was among the first radiative transfer codes to accurately
simulate the hemispherical reflectance and transmittance of various
plant leaves (monocots, dicots or senescent leaves) over the solar
spectrum from 400 nm to 2500 nm. Several versions have been made
widely available in the community (Fourty et al., 1996; Jacquemoud
et al., 1996; Baret and Fourty, 1997; Fourty and Baret, 1998;
Jacquemoud et al., 2000) and validated on different datasets.
The
first plate model was introduced by Allen
et al. (1969) who represented a leaf as an absorbing plate
with rough surfaces giving rise to Lambertian diffusion. Parameters
here are an index of refraction and an absorption coefficient.
This model was successful in reproducing the reflectance spectrum
of a compact corn leaf characterised by few air-cell wall interfaces.
The same authors rapidly extended the model to non-compact leaves
by regarding them as piles of N plates separated by N-1 air spaces
(Allen et al., 1970). The solution
of such a system, provided in the last century by Stokes (1862),
has been extended to N being a real number: this is the so-called
generalised plate model. This additional parameter N actually
describes the leaf internal structure and plays a role similar
to that of the scattering coefficients in the Kubelka-Munk model.
Now in widespread use in the remote sensing community, the PROSPECT model (Leaf Optical Properties
Spectra) has been designed this way (Jacquemoud and Baret,
1990). It was among the first radiative transfer codes to accurately
simulate the hemispherical reflectance and transmittance of various
plant leaves (monocots, dicots or senescent leaves) over the solar
spectrum from 400 nm to 2500 nm. Several versions have been made
widely available in the community (Fourty et al., 1996; Jacquemoud
et al., 1996; Baret and Fourty, 1997; Fourty and Baret, 1998;
Jacquemoud et al., 2000) and validated on different datasets.
- Version 2.01. Five input parameters: leaf structure
parameter (N), chlorophylls a+b concentration (Cab in µg/cm2),
equivalent water thickness (Cw in cm), protein content (Cp in
g/cm2), and cellulose + lignin content (Cc in g/cm2). Fortran
code (10 April 1995) and IDL
code (20 March 2001, Author: Glenn J. Newnham).
- Version 3.01. Four input parameters: leaf structure
parameter N, chlorophylls a+b concentration (Cab in µg/cm2),
equivalent water thickness (Cw in cm), and dry matter content
(Cm in g/cm2). Fortran code
(5 May 1998) or Matlab 5.2
code (4 April 2000). The Matlab user interface allows to
simulate and visualize the leaf optical properties in real time:
type promat under Matlab to run it.
For more information about PROSPECT,
please contact Stéphane
Jacquemoud, Equipe de Géodésie et Gravimétrie,
Institut de Physique du Globe de Paris, Paris (France).
N-flux models
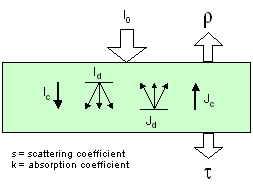 These models derived from
the Kubelka-Munk theory (Kubelka and Munk, 1931) consider the
leaf as a slab of diffusing (scattering coefficient s) and absorbing
(absorption coefficient k) material. The N-flux equations are
a simplification of the radiative transfer theory: the solution
of these equations yields simple analytical formulae for the diffuse
reflectance and transmittance. A two-flux model (Allen and Richardson,
1968) and a four-flux model (Fukshansky et al., 1991; Martinez
von Remisowsky et al., 1992; Richter and Fukshansky, 1996) have
been successfully used in the forward mode to calculate the s
and k optical parameters of plant leaves. Yamada and Fujimura
(1991) later proposed a more sophisticated version in which the
leaf was divided into four parallel layers: the upper cuticle,
the palisade parenchyma, the spongy mesophyll, and the lower cuticle.
The Kubelka-Munk theory is applied with different parameters in
each layer, and solutions are coupled with suitable boundary conditions
to provide the leaf reflectance and transmittance as a function
of the scattering and absorption coefficients. But these authors
went further, interpreting the absorption coefficient determined
in the visible region in terms of chlorophyll content. By inversion,
their model became a nondestructive method for the measurement
of photosynthetic pigments. The leaf biochemistry has been introduced
by Conel et al. (1993) who used a two-flux model to study the
influence of water, protein, cellulose, lignin, and starch on
leaf middle infrared reflectance. However they did not validate
it. Finally, a very simple model, directly issued from the expression
of the reflectance, has been used to estimate the chlorophyll
content of wheat leaves (Andrieu et al., 1988).
These models derived from
the Kubelka-Munk theory (Kubelka and Munk, 1931) consider the
leaf as a slab of diffusing (scattering coefficient s) and absorbing
(absorption coefficient k) material. The N-flux equations are
a simplification of the radiative transfer theory: the solution
of these equations yields simple analytical formulae for the diffuse
reflectance and transmittance. A two-flux model (Allen and Richardson,
1968) and a four-flux model (Fukshansky et al., 1991; Martinez
von Remisowsky et al., 1992; Richter and Fukshansky, 1996) have
been successfully used in the forward mode to calculate the s
and k optical parameters of plant leaves. Yamada and Fujimura
(1991) later proposed a more sophisticated version in which the
leaf was divided into four parallel layers: the upper cuticle,
the palisade parenchyma, the spongy mesophyll, and the lower cuticle.
The Kubelka-Munk theory is applied with different parameters in
each layer, and solutions are coupled with suitable boundary conditions
to provide the leaf reflectance and transmittance as a function
of the scattering and absorption coefficients. But these authors
went further, interpreting the absorption coefficient determined
in the visible region in terms of chlorophyll content. By inversion,
their model became a nondestructive method for the measurement
of photosynthetic pigments. The leaf biochemistry has been introduced
by Conel et al. (1993) who used a two-flux model to study the
influence of water, protein, cellulose, lignin, and starch on
leaf middle infrared reflectance. However they did not validate
it. Finally, a very simple model, directly issued from the expression
of the reflectance, has been used to estimate the chlorophyll
content of wheat leaves (Andrieu et al., 1988).
Compact spherical particle models
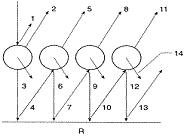 None of these models are
adapted to needle-shaped leaves due to a lack of experimental
data available on such targets. Dawson et al. (1998) adapted Melamed's
theory of light interaction with suspended powders (Melamed, 1963)
and designed the LIBERTY model
(Leaf Incorporating Biochemistry Exhibiting Reflectance and
Transmittance Yields) specifically to calculate the optical
properties of both dried and fresh stacked conifer (particularly
pine) needles. By treating the leaf as an aggregation of cells,
with multiple radiation scattering between cells, output reflectance
and transmittance spectra are a function of three structural parameters
(cell diameter in mm, intercellular air space, leaf thickness)
and the combined absorption coefficients of leaf biochemicals
(chlorophyll concentration in mg m-2, water content in g m-2,
lignin and cellulose content in g m-2, and nitrogen content in
g m-2). To date, LIBERTY remains the only model used for this
purpose.
None of these models are
adapted to needle-shaped leaves due to a lack of experimental
data available on such targets. Dawson et al. (1998) adapted Melamed's
theory of light interaction with suspended powders (Melamed, 1963)
and designed the LIBERTY model
(Leaf Incorporating Biochemistry Exhibiting Reflectance and
Transmittance Yields) specifically to calculate the optical
properties of both dried and fresh stacked conifer (particularly
pine) needles. By treating the leaf as an aggregation of cells,
with multiple radiation scattering between cells, output reflectance
and transmittance spectra are a function of three structural parameters
(cell diameter in mm, intercellular air space, leaf thickness)
and the combined absorption coefficients of leaf biochemicals
(chlorophyll concentration in mg m-2, water content in g m-2,
lignin and cellulose content in g m-2, and nitrogen content in
g m-2). To date, LIBERTY remains the only model used for this
purpose.
Radiative transfer theory
Compared with canopy level, only few models directly
use the radiative transfer equation at leaf level. The poor information
we have on leaf internal structure and biochemical distribution
leads to strong simplifications which make such an approach less
efficient as compared to more robust formulations. In Ma et al.
(1990), the leaf is described as a slab of water with an irregular
surface containing randomly distributed spherical particles. In
LEAFMOD (Leaf Experimental
Absorptivity Feasibility MODel), it is compared to a homogeneous
mixture of biochemicals which scatter and absorb light (Ganapol
et al., 1998). Each model was able to provide a faithful simulation
of leaf optical properties.
Stochastic models
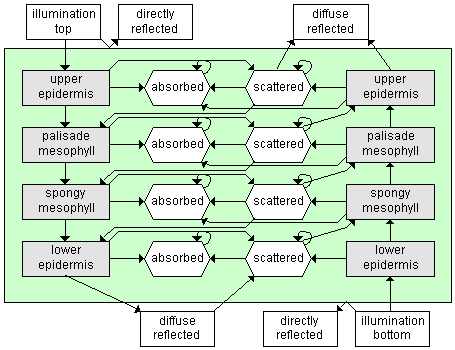
Tucker and Garatt (1977) proposed an original stochastic
model, LFMOD1, where the radiation
transfer is simulated by a Markov chain. A black maple leaf is
partitioned into two independent tissues, a palisade parenchyma
and a spongy mesophyll. Four radiation states (solar, reflected,
absorbed, and transmitted) are defined, as well as the transition
probabilities from one radiation state to another, between the
different compartments. These probabilities are set on the basis
of the optical properties of the leaf material. Starting with
an initial state vector representing the incident radiation, the
steady state is computed by iteratively applying the one-step
transition matrix, and yields both the reflectance and transmittance.
The SLOP (Stochastic
model for Leaf Optical Properties) model (Maier et al., 1999;
Maier, 2000) is an improved version of the stochastic model, which
differs in that the leaf is partitioned into four different tissues.
Ray tracing models
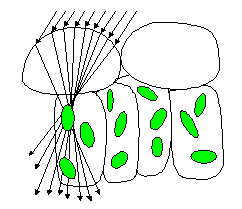 Among various approaches,
only ray tracing techniques can account for the complexity of
internal leaf structure as it appears in a photomicrograph. They
require a detailed description of individual cells and their unique
arrangement inside tissues. The optical constants of leaf materials
(cell walls, cytoplasm, pigments, air cavities, etc.) also have
to be defined. Using the laws of reflection, refraction, and absorption,
it is then possible to simulate the propagation of individual
photons incident on the leaf surface. Once a sufficient number
of rays have been simulated, statistically-valid estimates of
the radiation transfer in a leaf may be deduced. The technique
has been applied with a number of variants. The first studies
were performed at the cell level (Haberlandt, 1914; Gabrys-Mizera,
1976), in particular with epidermal cells the shape of which might
influence the path of the incident beams. Research efforts were
also directed toward understanding the transmission path of light
through entire leaves: Allen et al. (1973), and afterwards Brakke
and Smith (1987) modeled an albino maple leaf by 100 circular
arcs and of two media: intercellular space air and cell walls
characterised by their indices of refraction. The model was used
to test the specular and the diffuse nature of the reflection
at the cell walls. Simulations led to an underestimation of the
reflectance and an overestimation of the transmittance in the
near-infrared plateau, which was demonstrated shortly afterwards
by Kumar and Silva (1973) who found that the actual reflectance
and transmittance could be better reproduced by adding two more
media into the model, cytoplasm and chloroplasts, thereby increasing
the internal diffusion. Whatever the approach, the absorption
phenomena that characterise leaf optical properties outside the
near-infrared plateau has been ignored. Moreover in all these
models, leaves were always described as two-dimensional objects
although the three-dimensional structure of these organs is very
important to their physiological function.
Among various approaches,
only ray tracing techniques can account for the complexity of
internal leaf structure as it appears in a photomicrograph. They
require a detailed description of individual cells and their unique
arrangement inside tissues. The optical constants of leaf materials
(cell walls, cytoplasm, pigments, air cavities, etc.) also have
to be defined. Using the laws of reflection, refraction, and absorption,
it is then possible to simulate the propagation of individual
photons incident on the leaf surface. Once a sufficient number
of rays have been simulated, statistically-valid estimates of
the radiation transfer in a leaf may be deduced. The technique
has been applied with a number of variants. The first studies
were performed at the cell level (Haberlandt, 1914; Gabrys-Mizera,
1976), in particular with epidermal cells the shape of which might
influence the path of the incident beams. Research efforts were
also directed toward understanding the transmission path of light
through entire leaves: Allen et al. (1973), and afterwards Brakke
and Smith (1987) modeled an albino maple leaf by 100 circular
arcs and of two media: intercellular space air and cell walls
characterised by their indices of refraction. The model was used
to test the specular and the diffuse nature of the reflection
at the cell walls. Simulations led to an underestimation of the
reflectance and an overestimation of the transmittance in the
near-infrared plateau, which was demonstrated shortly afterwards
by Kumar and Silva (1973) who found that the actual reflectance
and transmittance could be better reproduced by adding two more
media into the model, cytoplasm and chloroplasts, thereby increasing
the internal diffusion. Whatever the approach, the absorption
phenomena that characterise leaf optical properties outside the
near-infrared plateau has been ignored. Moreover in all these
models, leaves were always described as two-dimensional objects
although the three-dimensional structure of these organs is very
important to their physiological function.
 For this reason, Govaerts
et al. (1996) used a three-dimensional ray tracing model, RAYTRAN (Govaerts and Verstraete,
1998), on a virtual 3D dorsiventral leaf, to characterise the
light environment, including absorption, scattering and transmission,
within and between cells: Cells of variable size, cell wall thicknesses,
chemistry and air spaces were modeled and implications for absorption
profiles, light harvesting, and photosynthesis were successfully
investigated (Ustin et al., 2001). Finally, in a completely different
domain, namely image synthesis, modeling of light interaction
with biological tissues such as plant leaves recently emerged
with ABM (Algorithmic BDF
Model) (Baranoski and Rokne, 1997, 1999).
For this reason, Govaerts
et al. (1996) used a three-dimensional ray tracing model, RAYTRAN (Govaerts and Verstraete,
1998), on a virtual 3D dorsiventral leaf, to characterise the
light environment, including absorption, scattering and transmission,
within and between cells: Cells of variable size, cell wall thicknesses,
chemistry and air spaces were modeled and implications for absorption
profiles, light harvesting, and photosynthesis were successfully
investigated (Ustin et al., 2001). Finally, in a completely different
domain, namely image synthesis, modeling of light interaction
with biological tissues such as plant leaves recently emerged
with ABM (Algorithmic BDF
Model) (Baranoski and Rokne, 1997, 1999).
Despite decades of research, much more work is required
before we will accurately model leaf optical properties. Models
are nevertheless essential to understand how electromagnetic radiation
interacts with leaf elements, but also to directly relate observed
optical properties to leaf biophysical attributes.
References
- Allen W.A. and Richardson A.J. (1968), Interaction
of light with a plant canopy, Journal of the Optical Society
of America, 58(8):1023-1028.
- Allen W.A., Gausman H.W., Richardson A.J.
and Thomas J.R. (1969), Interaction of isotropic light with a
compact plant leaf, Journal of the Optical Society of America,
59(10):1376-1379.
- Allen W.A., Gausman H.W. and Richardson A.J.
(1970), Mean effective optical constants of cotton leaves, Journal
of the Optical Society of America, 60(4):542-547.
- Allen W.A., Gausman H.W. and Richardson A.J.
(1973), Willstatter-Stoll theory of leaf reflectance evaluated
by ray tracing, Applied Optics, 12(10):2448-2453.
- Andrieu B., Baret F., Schellberg J. and Rinderle
U. (1988), Estimation de spectres de feuilles à partir
de mesures dans les bandes spectrales larges, in Proc. 4th
International Colloquium on Spectral Signatures of Objects in
Remote Sensing, Aussois (France), 18-22 January 1988, ESA,
Vol. SP-287, pp. 351-356.
- Baranoski G.V.B. and Rokne J.G. (1997), An
algorithmic reflectance and transmittance model for plant tissue,
in Proc. Conference of the European Association for Computer
Graphics (Eurographics'97) (D. Fellner & L. Szirmay-Kalos,
eds), Budapest (Hungary), Vol. 16(3), pp. 141-150.
- Baranoski G.V.G. and Rokne J.G. (1999), A
non-deterministic reconstruction approach for isotropic reflectances
and transmittances, Journal of Visualization and Computer
Animation, 10(4):225-231.
- Baret F. and Fourty T. (1997), Estimation
of leaf water content and specific leaf weight from reflectance
and transmittance measurements, Agronomie, 17(9-10):455-464.
- Brakke T.W. and Smith J.A. (1987), A ray
tracing model for leaf bidirectional scattering studies, in Proc.
7th International Geoscience and Remote Sensing Symposium (IGARSS'87),
Ann Arbor (MI), 18-21 May 1987, IEEE, pp. 643-648.
- Conel J.E., Bosch J.v.d. and Grove C.I. (1993),
Application of a two-stream radiative transfer model for leaf
lignin and cellulose concentrations from spectral reflectance
measurements. Part 1, in Proc. 4th Annual JPL Geoscience Workshop:
AVIRIS (R.O. Green, ed), Washington (DC), 25-29 October 1993,
NASA-JPL Publication, Vol. 93-26, pp. 39-43.
- Dawson T.P., Curran P.J. and Plummer S.E.
(1998), LIBERTY - Modeling the effects of leaf biochemical concentration
on reflectance spectra, Remote Sensing of Environment,
65(1):50-60.
- Fourty T., Baret F., Jacquemoud S., Schmuck
G. and Verdebout J. (1996), Optical properties of dry plant leaves
with explicite description of their biochemical composition:
direct and inverse problems, Remote Sensing of Environment,
56(2):104-117.
- Fourty T. and Baret F. (1998), On spectral
estimates of fresh leaf biochemistry, International Journal
of Remote Sensing, 19(7):1283-1297.
- Fukshansky L., Fukshansky-Kazarinova N. and
Martinez v. Remisowsky A.M. (1991), Estimation of optical parameters
in a living tissue by solving the inverse problem of the multiflux
radiative transfer, Applied Optics, 30(22):3145-3153.
- Gabrys-Mizera H. (1976), Model considerations
of the light conditions in noncylindrical plant cells, Photochemistry
and Photobiology, 24:453-461.
- Ganapol B.D., Johnson L.F., Hammer P.D.,
Hlavka C.A. and Peterson D.L. (1998), LEAFMOD: a new within-leaf
radiative transfer model, Remote Sensing of Environment,
63(2):182-193.
- Govaerts Y., Jacquemoud S., Verstraete M.M.
and Ustin S.L. (1996), Three-dimensional radiation transfer modeling
in a dicotyledon leaf, Applied Optics, 35(33):6585-6598.
- Govaerts Y. and Verstraete M.M. (1998), Raytran:
a Monte Carlo ray-tracing model to compute light scattering in
three-dimensional heterogeneous media, IEEE Transactions on
Geoscience and Remote Sensing, 36(2):493-505.
- Haberlandt G. (1914), Optical sense-organs,
in Physiological Plant Anatomy (G. Haberlandt, ed), MacMillan
and Co., London, pp. 613-631.
- Jacquemoud S. and Baret F. (1990), PROSPECT:
a model of leaf optical properties spectra, Remote Sensing
of Environment, 34:75-91.
- Jacquemoud S., Ustin S.L., Verdebout J.,
Schmuck G., Andreoli G. and Hosgood B. (1996), Estimating leaf
biochemistry using the PROSPECT leaf optical properties model,
Remote Sensing of Environment, 56(3):194-202.
- Jacquemoud S., Bacour C., Poilvé H.
and Frangi J.-P. (2000), Comparison of four radiative transfer
models to simulate plant canopies reflectance - Direct and inverse
mode, Remote Sensing of Environment, 74:471-481.
- Kubelka P. and Munk F. (1931), Ein beitrag
zur optik der farbanstriche, Zeitschrift fur Technische Physik,
12:593-601.
- Kumar R. and Silva L. (1973), Light ray tracing
through a leaf cross section, Applied Optics, 12(12):2950-2954.
- Ma Q., Ishimaru A., Phu P. and Kuga Y. (1990),
Transmission, reflection, and depolarization of an optical wave
for a single leaf, IEEE Transactions on Geoscience and Remote
Sensing, 28(5):865-872.
- Maier S.W., Lüdeker W. and Günther
K.P. (1999), SLOP: a revised version of the stochastic model
for leaf optical properties, Remote Sensing of Environment,
68(3):273-280.
- Maier S.W. (2000), Modeling the radiative
transfer in leaves in the 300 nm to 2.5 µm wavelength region
taking into consideration chlorophyll fluorescence - The leaf
model SLOPE, PhD Thesis, Deutsches Fernerkundungstagsdatenzentrum,
Technische Universität München, Oberpfaffenhofen (Germany),
110 pp.
- Martinez von Remisowsky A., McClendon J.H.
and Fukshansky L. (1992), Estimation of the optical parameters
and light gradients in leaves: multi-flux versus two-flux treatement,
Photochemistry and Photobiology, 55(6):857-865.
- Melamed N.T. (1963), Optical properties of
powders. Part I. Optical absorption coefficients and the absolute
value of the diffuse reflectance. Part II. Properties of luminescent
powders, Applied Optics, 34(3):560-570.
- Richter T. and Fukshansky L. (1996), Optics
of a bifacial leaf: 1. A novel combined procedure for deriving
the optical parameters, Photochemistry and Photobiology,
63(4):507-516.
- Stokes G.G. (1862), On the intensity of the
light reflected from or transmitted through a pile of plates,
Proceedings of the Royal Society of London. Series B,
11:545-556.
- Tucker C.J. and Garratt M.W. (1977), Leaf
optical system modeled as a stochastic process, Applied Optics,
16(3):635-642.
- Ustin S.L., Jacquemoud S. and Govaerts Y.
(2001), Simulation of photon transport in a three-dimensional
leaf: implications for photosynthesis, Plant, Cell & Environment,
24:1095-1103.
- Yamada N. and Fujimura S. (1991), Nondestructive
measurement of chlorophyll pigment content in plant leaves from
three-color reflectance and transmittance, Applied Optics,
30(27):3964-3973.

 The
first plate model was introduced by Allen
et al. (1969) who represented a leaf as an absorbing plate
with rough surfaces giving rise to Lambertian diffusion. Parameters
here are an index of refraction and an absorption coefficient.
This model was successful in reproducing the reflectance spectrum
of a compact corn leaf characterised by few air-cell wall interfaces.
The same authors rapidly extended the model to non-compact leaves
by regarding them as piles of N plates separated by N-1 air spaces
(Allen et al., 1970). The solution
of such a system, provided in the last century by Stokes (1862),
has been extended to N being a real number: this is the so-called
generalised plate model. This additional parameter N actually
describes the leaf internal structure and plays a role similar
to that of the scattering coefficients in the Kubelka-Munk model.
Now in widespread use in the remote sensing community, the PROSPECT model (Leaf Optical Properties
Spectra) has been designed this way (Jacquemoud and Baret,
1990). It was among the first radiative transfer codes to accurately
simulate the hemispherical reflectance and transmittance of various
plant leaves (monocots, dicots or senescent leaves) over the solar
spectrum from 400 nm to 2500 nm. Several versions have been made
widely available in the community (Fourty et al., 1996; Jacquemoud
et al., 1996; Baret and Fourty, 1997; Fourty and Baret, 1998;
Jacquemoud et al., 2000) and validated on different datasets.
The
first plate model was introduced by Allen
et al. (1969) who represented a leaf as an absorbing plate
with rough surfaces giving rise to Lambertian diffusion. Parameters
here are an index of refraction and an absorption coefficient.
This model was successful in reproducing the reflectance spectrum
of a compact corn leaf characterised by few air-cell wall interfaces.
The same authors rapidly extended the model to non-compact leaves
by regarding them as piles of N plates separated by N-1 air spaces
(Allen et al., 1970). The solution
of such a system, provided in the last century by Stokes (1862),
has been extended to N being a real number: this is the so-called
generalised plate model. This additional parameter N actually
describes the leaf internal structure and plays a role similar
to that of the scattering coefficients in the Kubelka-Munk model.
Now in widespread use in the remote sensing community, the PROSPECT model (Leaf Optical Properties
Spectra) has been designed this way (Jacquemoud and Baret,
1990). It was among the first radiative transfer codes to accurately
simulate the hemispherical reflectance and transmittance of various
plant leaves (monocots, dicots or senescent leaves) over the solar
spectrum from 400 nm to 2500 nm. Several versions have been made
widely available in the community (Fourty et al., 1996; Jacquemoud
et al., 1996; Baret and Fourty, 1997; Fourty and Baret, 1998;
Jacquemoud et al., 2000) and validated on different datasets. These models derived from
the Kubelka-Munk theory (Kubelka and Munk, 1931) consider the
leaf as a slab of diffusing (scattering coefficient s) and absorbing
(absorption coefficient k) material. The N-flux equations are
a simplification of the radiative transfer theory: the solution
of these equations yields simple analytical formulae for the diffuse
reflectance and transmittance. A two-flux model (Allen and Richardson,
1968) and a four-flux model (Fukshansky et al., 1991; Martinez
von Remisowsky et al., 1992; Richter and Fukshansky, 1996) have
been successfully used in the forward mode to calculate the s
and k optical parameters of plant leaves. Yamada and Fujimura
(1991) later proposed a more sophisticated version in which the
leaf was divided into four parallel layers: the upper cuticle,
the palisade parenchyma, the spongy mesophyll, and the lower cuticle.
The Kubelka-Munk theory is applied with different parameters in
each layer, and solutions are coupled with suitable boundary conditions
to provide the leaf reflectance and transmittance as a function
of the scattering and absorption coefficients. But these authors
went further, interpreting the absorption coefficient determined
in the visible region in terms of chlorophyll content. By inversion,
their model became a nondestructive method for the measurement
of photosynthetic pigments. The leaf biochemistry has been introduced
by Conel et al. (1993) who used a two-flux model to study the
influence of water, protein, cellulose, lignin, and starch on
leaf middle infrared reflectance. However they did not validate
it. Finally, a very simple model, directly issued from the expression
of the reflectance, has been used to estimate the chlorophyll
content of wheat leaves (Andrieu et al., 1988).
These models derived from
the Kubelka-Munk theory (Kubelka and Munk, 1931) consider the
leaf as a slab of diffusing (scattering coefficient s) and absorbing
(absorption coefficient k) material. The N-flux equations are
a simplification of the radiative transfer theory: the solution
of these equations yields simple analytical formulae for the diffuse
reflectance and transmittance. A two-flux model (Allen and Richardson,
1968) and a four-flux model (Fukshansky et al., 1991; Martinez
von Remisowsky et al., 1992; Richter and Fukshansky, 1996) have
been successfully used in the forward mode to calculate the s
and k optical parameters of plant leaves. Yamada and Fujimura
(1991) later proposed a more sophisticated version in which the
leaf was divided into four parallel layers: the upper cuticle,
the palisade parenchyma, the spongy mesophyll, and the lower cuticle.
The Kubelka-Munk theory is applied with different parameters in
each layer, and solutions are coupled with suitable boundary conditions
to provide the leaf reflectance and transmittance as a function
of the scattering and absorption coefficients. But these authors
went further, interpreting the absorption coefficient determined
in the visible region in terms of chlorophyll content. By inversion,
their model became a nondestructive method for the measurement
of photosynthetic pigments. The leaf biochemistry has been introduced
by Conel et al. (1993) who used a two-flux model to study the
influence of water, protein, cellulose, lignin, and starch on
leaf middle infrared reflectance. However they did not validate
it. Finally, a very simple model, directly issued from the expression
of the reflectance, has been used to estimate the chlorophyll
content of wheat leaves (Andrieu et al., 1988). None of these models are
adapted to needle-shaped leaves due to a lack of experimental
data available on such targets. Dawson et al. (1998) adapted Melamed's
theory of light interaction with suspended powders (Melamed, 1963)
and designed the LIBERTY model
(Leaf Incorporating Biochemistry Exhibiting Reflectance and
Transmittance Yields) specifically to calculate the optical
properties of both dried and fresh stacked conifer (particularly
pine) needles. By treating the leaf as an aggregation of cells,
with multiple radiation scattering between cells, output reflectance
and transmittance spectra are a function of three structural parameters
(cell diameter in mm, intercellular air space, leaf thickness)
and the combined absorption coefficients of leaf biochemicals
(chlorophyll concentration in mg m-2, water content in g m-2,
lignin and cellulose content in g m-2, and nitrogen content in
g m-2). To date, LIBERTY remains the only model used for this
purpose.
None of these models are
adapted to needle-shaped leaves due to a lack of experimental
data available on such targets. Dawson et al. (1998) adapted Melamed's
theory of light interaction with suspended powders (Melamed, 1963)
and designed the LIBERTY model
(Leaf Incorporating Biochemistry Exhibiting Reflectance and
Transmittance Yields) specifically to calculate the optical
properties of both dried and fresh stacked conifer (particularly
pine) needles. By treating the leaf as an aggregation of cells,
with multiple radiation scattering between cells, output reflectance
and transmittance spectra are a function of three structural parameters
(cell diameter in mm, intercellular air space, leaf thickness)
and the combined absorption coefficients of leaf biochemicals
(chlorophyll concentration in mg m-2, water content in g m-2,
lignin and cellulose content in g m-2, and nitrogen content in
g m-2). To date, LIBERTY remains the only model used for this
purpose.
 Among various approaches,
only ray tracing techniques can account for the complexity of
internal leaf structure as it appears in a photomicrograph. They
require a detailed description of individual cells and their unique
arrangement inside tissues. The optical constants of leaf materials
(cell walls, cytoplasm, pigments, air cavities, etc.) also have
to be defined. Using the laws of reflection, refraction, and absorption,
it is then possible to simulate the propagation of individual
photons incident on the leaf surface. Once a sufficient number
of rays have been simulated, statistically-valid estimates of
the radiation transfer in a leaf may be deduced. The technique
has been applied with a number of variants. The first studies
were performed at the cell level (Haberlandt, 1914; Gabrys-Mizera,
1976), in particular with epidermal cells the shape of which might
influence the path of the incident beams. Research efforts were
also directed toward understanding the transmission path of light
through entire leaves: Allen et al. (1973), and afterwards Brakke
and Smith (1987) modeled an albino maple leaf by 100 circular
arcs and of two media: intercellular space air and cell walls
characterised by their indices of refraction. The model was used
to test the specular and the diffuse nature of the reflection
at the cell walls. Simulations led to an underestimation of the
reflectance and an overestimation of the transmittance in the
near-infrared plateau, which was demonstrated shortly afterwards
by Kumar and Silva (1973) who found that the actual reflectance
and transmittance could be better reproduced by adding two more
media into the model, cytoplasm and chloroplasts, thereby increasing
the internal diffusion. Whatever the approach, the absorption
phenomena that characterise leaf optical properties outside the
near-infrared plateau has been ignored. Moreover in all these
models, leaves were always described as two-dimensional objects
although the three-dimensional structure of these organs is very
important to their physiological function.
Among various approaches,
only ray tracing techniques can account for the complexity of
internal leaf structure as it appears in a photomicrograph. They
require a detailed description of individual cells and their unique
arrangement inside tissues. The optical constants of leaf materials
(cell walls, cytoplasm, pigments, air cavities, etc.) also have
to be defined. Using the laws of reflection, refraction, and absorption,
it is then possible to simulate the propagation of individual
photons incident on the leaf surface. Once a sufficient number
of rays have been simulated, statistically-valid estimates of
the radiation transfer in a leaf may be deduced. The technique
has been applied with a number of variants. The first studies
were performed at the cell level (Haberlandt, 1914; Gabrys-Mizera,
1976), in particular with epidermal cells the shape of which might
influence the path of the incident beams. Research efforts were
also directed toward understanding the transmission path of light
through entire leaves: Allen et al. (1973), and afterwards Brakke
and Smith (1987) modeled an albino maple leaf by 100 circular
arcs and of two media: intercellular space air and cell walls
characterised by their indices of refraction. The model was used
to test the specular and the diffuse nature of the reflection
at the cell walls. Simulations led to an underestimation of the
reflectance and an overestimation of the transmittance in the
near-infrared plateau, which was demonstrated shortly afterwards
by Kumar and Silva (1973) who found that the actual reflectance
and transmittance could be better reproduced by adding two more
media into the model, cytoplasm and chloroplasts, thereby increasing
the internal diffusion. Whatever the approach, the absorption
phenomena that characterise leaf optical properties outside the
near-infrared plateau has been ignored. Moreover in all these
models, leaves were always described as two-dimensional objects
although the three-dimensional structure of these organs is very
important to their physiological function. For this reason, Govaerts
et al. (1996) used a three-dimensional ray tracing model, RAYTRAN (Govaerts and Verstraete,
1998), on a virtual 3D dorsiventral leaf, to characterise the
light environment, including absorption, scattering and transmission,
within and between cells: Cells of variable size, cell wall thicknesses,
chemistry and air spaces were modeled and implications for absorption
profiles, light harvesting, and photosynthesis were successfully
investigated (Ustin et al., 2001). Finally, in a completely different
domain, namely image synthesis, modeling of light interaction
with biological tissues such as plant leaves recently emerged
with ABM (Algorithmic BDF
Model) (Baranoski and Rokne, 1997, 1999).
For this reason, Govaerts
et al. (1996) used a three-dimensional ray tracing model, RAYTRAN (Govaerts and Verstraete,
1998), on a virtual 3D dorsiventral leaf, to characterise the
light environment, including absorption, scattering and transmission,
within and between cells: Cells of variable size, cell wall thicknesses,
chemistry and air spaces were modeled and implications for absorption
profiles, light harvesting, and photosynthesis were successfully
investigated (Ustin et al., 2001). Finally, in a completely different
domain, namely image synthesis, modeling of light interaction
with biological tissues such as plant leaves recently emerged
with ABM (Algorithmic BDF
Model) (Baranoski and Rokne, 1997, 1999).